기하학 역설-2

2023.10.05 - [수학] - 기하학 역설-1

 

기하학 역설-1

 

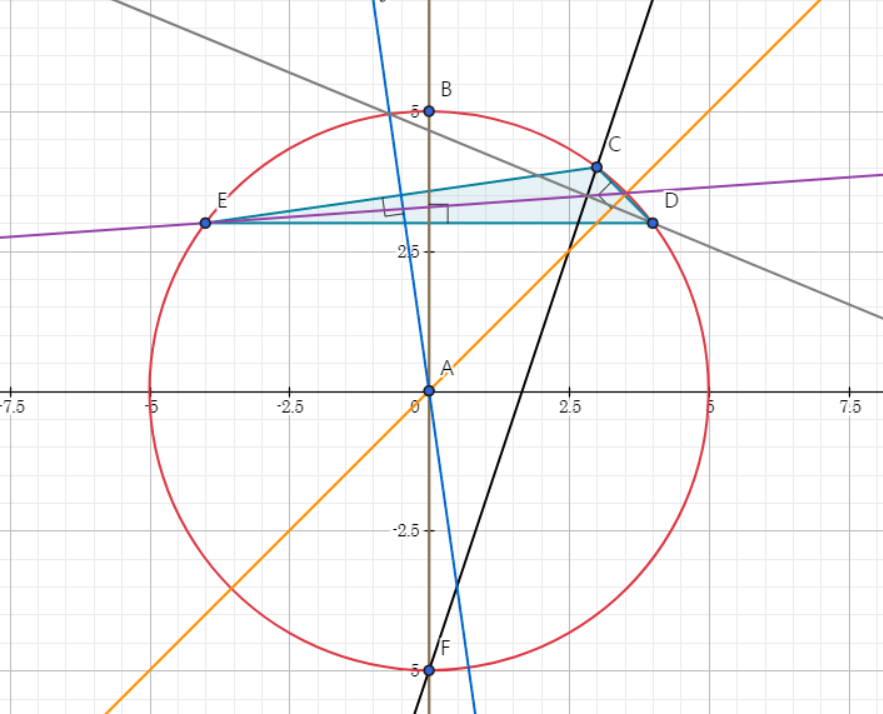
이렇게 모든 변에 대하여 적용이 가능하다. 이렇게 보면 내심과 외심까지도 관찰이 가능하다.

 

그럼 그 교점들은 연결하여 만든 삼각형은 원래의 삼각형과 어떤 관련이 있을까?

이를 더 여러번 반복하면 뭔가 정삼각형이 되어가는 듯이 보인다. 임의의 수열 $0<a_n<b_n<c_n<2{\pi}$을 가지고 오자. ${\frac{a_n+b_n}{2}}, {\frac{b_n+c_n}{2}} , {\frac{c_n+a_n}{2}} +{\pi}$을 각각 작은 순서대로 $a_{n+1},b_{n+1},c_{n+1}$ 로 정의하여야한다. 이 수열이 정렬되어 있지 않으면 더 복잡해진다. 여기서 각각의 극한 값을 구했을 때, 어디로 수렴하냐에 문제로 바꿀 수 있다.

문제의 식만 보면, https://ghebook.blogspot.com/2010/07/intermediate-value-theorem.html

증명 과정에 있는 상황과 아주 비슷하다. 그러나 이 문제에서는 수열이 정렬이 필요하다는 큰 복잡성을 가지고 있다.

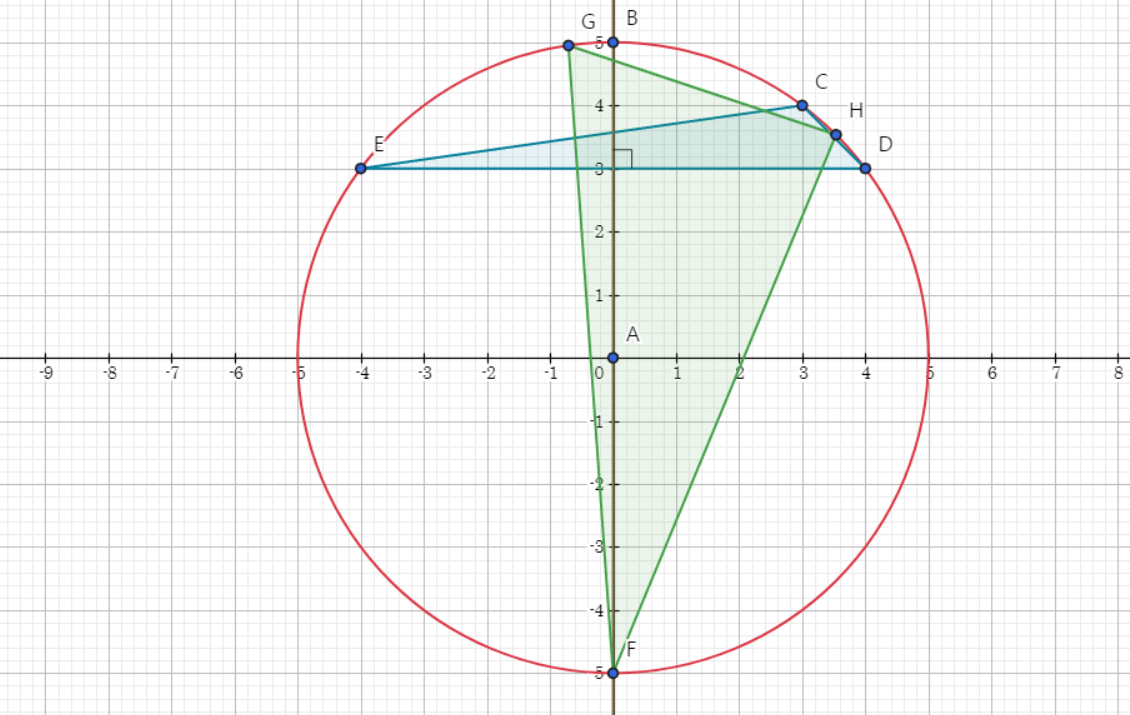
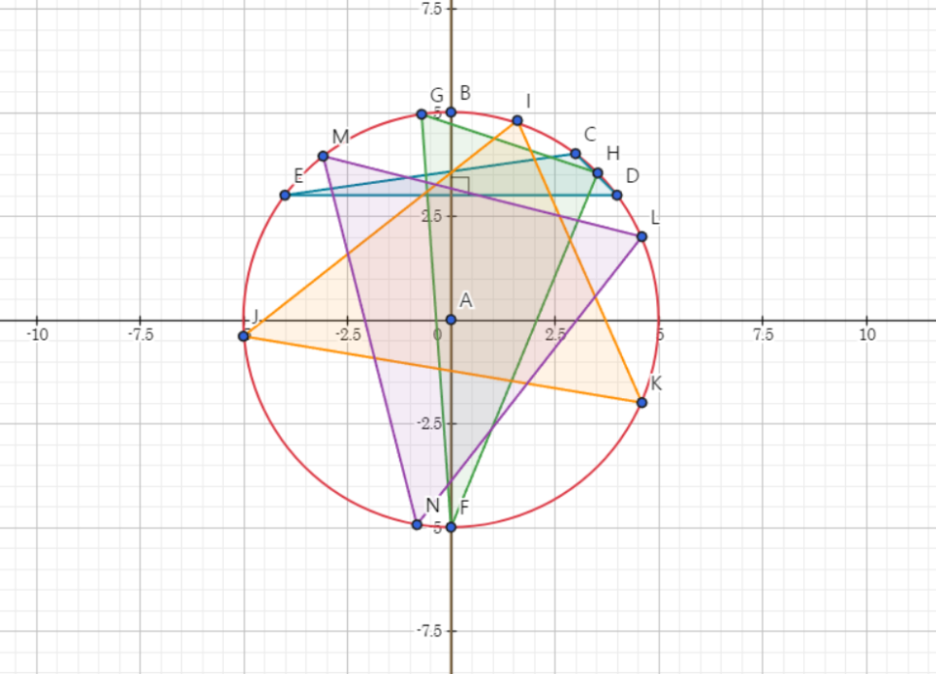
#include <iostream>
#include <algorithm>
int main() {
	double a[3];
	std::cout << "구간 [0,2)에 서로 다른 세 실수를 입력하세요";
	std::cin >> a[0] >> a[1] >> a[2];
	for (int i = 0; i < 100; i++) {
		std::sort(a + 0, a + 3);
		std::cout << abs(a[1]-a[0]) << " " << abs(a[2] - a[1]) << " " << abs(2-(a[2] - a[0])) << "\n";
		double t[3];
		for (int j = 0; j < 3; j++) {
			t[j] = (a[j % 3] + a[(j + 1) % 3]) / 2 + (j==2);
			if (t[j] > 2) t[j] -= 2;
		}
		for (int j = 0; j < 3; j++) a[j] = t[j];
	}
}

이런 식으로 코드를 만들어서 구현을 해보면, 초기 값에 무엇을 넣던 항상 그 차이가 0.6667(2/3일 것으로 추정)으로 수렴한다는 것을 확인할 수는 있다.

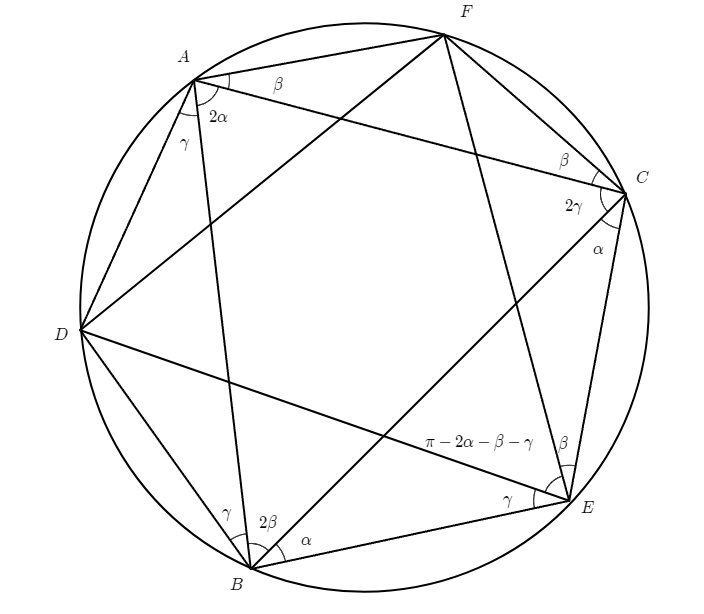
처음 삼각형의 각도를 $2{\alpha},2{\beta},2{\gamma}$라고 해보면 원주각의 관계를 이용하여서 다음에 만들어지는 삼각형의 각도는 각각

${\pi}-(2{\alpha}+{\beta}+{\gamma})\;,{\pi}-({\alpha}+2{\beta}+{\gamma});,{\pi}-({\alpha}+{\beta}+2{\gamma})$ 가 되고,

여기서 $2{\alpha}+2{\beta}+2{\gamma}=2{\pi}$였기 때문에

다시 ${\frac{{\pi}}{2}}-{\alpha}\;,{\frac{{\pi}}{2}}-{\beta}\;,{\frac{{\pi}}{2}}-{\gamma}$가 된다는 것을 알 수 있다.

이를 연쇄적으로 했을 때, 각도는 $ {\frac{{\pi}}{2}}- {\frac{{\pi}}{4}}+{\frac{{\pi}}{8}}-....$이 된다. 이 등비급수의 합은 ${\frac{{\pi}}{3}}$으로 수렴한다. 이렇게 각도 관계를 이용하여 정삼각형에 가까워 진다는 것을 증명할 수 있다. 그림상으로는 예각삼각형으로 표현하였지만, 얼마든지 둔각도 가능하다.

또한 처음의 삼각형의 넓이를 구하면 $2r^2(sin2{\alpha})(sin2{\beta})(sin2{\gamma})$ 즉 인데, 두 번째 삼각형은 $2r^2(cos{\alpha})(cos{\beta})(cos{\gamma})$가 된다. 덧셈 정리를 이용해서 넓이 비는 $8sin({\alpha})sin({\beta})sin({\gamma})$가 됨을 알 수 있다. 사각형도 비슷하게 될 거 같다.