기하학 역설-1

 

다음과 같이 수학에는 기하학의 역설이라는 내용이 있다.

 

기하학의 역설에서는 삼각형 한변의 수직이등분선과 그 대각의 이등분선의 교점에 대한 논리를 이용하는 경우가 많다. 그 경우에는 수직이등분선과 각이등분선의 교점이 삼각형 내부에서 만나는 것처럼 그림을 그려서 역설을 발생시킨다. 하지만 실제로는 항상 "삼각형에서 한 변의 수직이등분선과 대각의 각이등분선의 교점은 두 선이 일치하지 않으면 항상 삼각형 외부에서 만난다." 이는 삼각형의 각의 이등분선 정리를 참고하면 지극히 자명하다.

 

https://mathbang.net/173

삼각형의 각의 이등분선과 닮음

 

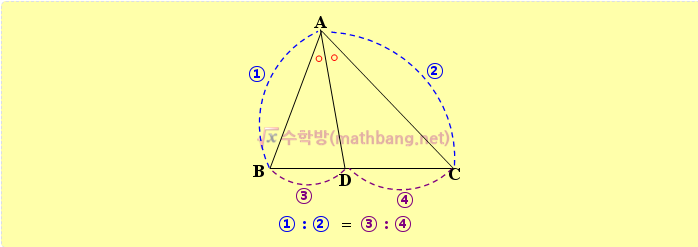
삼각형에서 (1)이(2) 와 같다면 선분bc와 선분ad는 수직이 되고, (3)과(4)도 같을 것이다. 이 경우에는 수직이등분선과 그 대각의이등분선이 일치하기 때문에 교점을 판단할 수 없다.(부정)

삼각형에서 (2)이 (1)보다 크다면 선분bc의 중점은 선분cd위에 존재할 수 밖에 없고, 그림과같은 상황이 되기 때문에 외부에 존재할 수 밖에 없다.(1이 더 큰 경우도 대칭적인 상황이기 때문에 외부에 존재한다.)

 

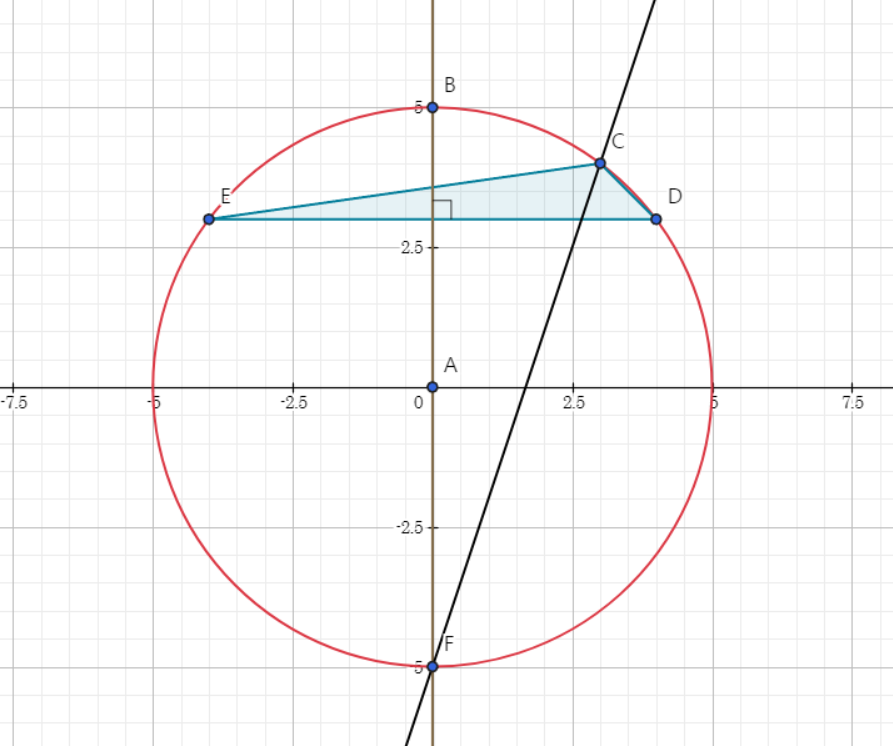
사실 원에서도 증명을 할 수 있다.

 

임의의 현을 잡고 그 변의 수직이등분선과 대각의 이등분선의 교점은 항상 수직이등분선과 원의 교점이라는 것을 원주각의 성질을 이용하면 아주 쉽게 알 수 있다.