[수능 지구과학2] 해파 속도

 

서론

 

     우리가 파동에 대해 배울 때를 생각해보자. 처음에 배우는 내용은 아마 파동은 에너지가 전달 되는 것이지 매질이 전달되지 않는다는 것이다. 따라서 해파의 경우 물입자는 이동하지 않고, 단순히 위아래로 진동한다고 배운다. 그러나 지2를 하면 물입자는 원운동을 한다고 배운다. 여기까지는 사실 납득가능하다. 하지만 실제로는 분자가 위에 있을 수록 더 빠르게 이동하기 때문에 물입자는 파동운동 방향으로 조금씩 표류하게 된다. 이렇듯 유체를 현실과 가깝게 분석하는 일은 굉장히 어려운 일이다. 그래서 해파의 속도를 이론적으로 구하기 위해서는 굉장히 이상적인 가정들과 좋은 분석 툴이 필요하다. 그래서 미소진폭파 이론을 이용하여 지구과학2에 나오는 해파의 속도를 구할려고 한다.

미소진폭파

사진1 출처: 항만공학

 

파동이론에 있어서 G.B Airy는 1845년에 미소진폭파의 분산관계식을 제시하였으며, G.G Stokes는 1849년에 속도포텐셜을 사용하여 파 이론을 전개하였다. 한편 비선형파이론인 트로코이드파(trocodial wave)이론은 1802년에 Gerstner에 의하여 유도되었다. 규칙파를 이론적으로 취급할 때 진폭이 파장에 비해서 극히 작다고 가정하고, 물입자의 연직가속도를 작다고 하여 이것을 생략한다면 파동에 대한 운동방정식은 선형이 되고 이와 같은 파동을 미소진폭파라고 한다. 

1.유체밀도는 불변

2.수면인장은 무시

3.corioli's 영향은 무시

4.자유표면의 압력은 균등

5.비점성 유체

6.비회전류

7.해저는 수평,고정,불투성이어서 물입자의 연직속도가 해저에서 영

8.진폭이 작고 파형은 시간과 공간적으로 불변

9.연직 2차원 장봉파(평면)

 

 

속도 퍼텐셜

기본적으로 퍼텐셜 함수에 대해 알아야 한다.  $u(x,y)=(2x,2y)$라는 벡터함수가 있다고 해보자. $\varphi (x,y)=x^2+y^2$인 다변수함수를 생각해 보면 $u=\mathrm{\nabla }\varphi$로 나타낼 수 있다. 이 때 $\mathrm{\nabla }$는 Gradient라고 한다. 다변수 버전의 미분이라고 생각할 수 있다. 이 때 $u=\mathrm{\nabla }\varphi$를 만족하는 $\varphi$가 존재하면, $u$는 보존장이라고 하고, $\varphi$를 잠재 함수 또는 퍼텐셜 함수라고 한다. 중력이나 전자기력은 사실 보존장이다. 

$u$를 해수의 속도를 표현하는 벡터함수라고 하자. 사진1을 보면 $x,z$축만 고려하면 된다는 것을 알 수 있다.  $\mathrm{\nabla }\times u=0$(비회전 유동)이라고 가정한다. 이는 해파의 속도가 방향을 바꾸지 않고, 직선으로 이동한다는 것을 의미한다. 다른 말로는 물의 점성을 무시한다고도 할 수 있다. 점성없이 단순 자연력에 의한 운동은 회전하지 않기 때문이다. 이를 "u의 Curl이 0이다."라고도 한다. 일반적으로 $0=\mathrm{\nabla }\times \mathrm{\nabla }\varphi$가 성립한다. 그래서 $\mathrm{\nabla }\times u=0$이면 $u$가 보존장 즉, $\mathrm{\nabla }\varphi =u$을 만족하는 $\varphi$가 존재할 거라고 의심해볼 수 있다. 그리고 정의역이 '이쁘게' 생겼다면 존재성을 보장할 수 있다. 그리고 이 경우에는 존재한다.

따라서 $\varphi$를 속도 퍼텐셜함수라고 한다. 

또한 $\mathrm{\nabla }\cdot u=0$(연속 방정식)을 가정한다. 이 연산자는 Divergent로, 이 가정의 의미는 속도가 갑자기 증가하거나 감소하지 않는다는 것이다. 또 다른 말로는 물이 압축되지 않는다는 것을 의미한다. 더불어 $\mathrm{\nabla }\varphi =u$이기 때문에 $\mathrm{\nabla }\cdot \mathrm{\nabla }\varphi ={\mathrm{\nabla }}^2\varphi =0$이라고 쓸 수 있고, 이를 라플라스 방정식이라고 한다. 이 방정식이 해파의 거동을 지배한다고 할 수 있기 때문에 지배 방정식이라고 부른다. 

조건

그 이후로 여러 조건들이 필요하다. 이제 물리적 특성들을 고려하는 것이다. 특히 여기서는 경계조건을 이용한다. 

 

KBC

자유표면에서의 운동학적 조건(kinematic free boundary condition)이라고 불리는 조건을 이용한다. 자유 표면은 공기와 물사이의 경계를 의미한다. 자유표면의 방정식을 $z=\eta (x,t)$이라고 할 수 있다. (여기서 $z$는 $u$의 변수 $z$와는 다르다고 생각하는 것이 좋다.) 시간에 따라 자유 표면의 높이가 계속 달라지기도 하고, 위치에 따라서도 높이가 달라질 것이다. 파동방정식을 떠올리면 쉽게 이해할 수 있을 것이다.

$F(x,t,z)=\eta (x,t)-z=0$으로 다시 쓸 수도 있다.  $(z=\eta )$ 일 때 $\frac{DF}{Dt}=0$이여야만 한다. 다변수에 대한 연쇄법칙을 이용하면 $\frac{dF}{dt}=\frac{\partial F}{\partial t}+u\cdot \mathrm{\nabla }F=\frac{\partial F}{\partial t}+u_1\frac{\partial F}{\partial x}+u_2\frac{\partial F}{\partial z}$($u=(u_1,u_2)$)로 바꿀 수 있다. 여기서 $F(x,t,z)=\eta (x,t)-z$를 대입하면  $\frac{dF}{dt}=\frac{\partial \eta }{\partial t}+u_1\frac{\partial \eta }{\partial x}-u_2=0$으로 바꿀 수 있다. 여기에 잠재함수를 대입하면 $\frac{\partial \eta }{\partial t}+\frac{\partial \varphi }{\partial x}\frac{\partial \eta }{\partial x}-\frac{\partial \varphi }{\partial z}=0$ $(z=\eta )$

여기서  미소진폭파이기 때문에 테일러 전개를 이용할 수 있다. 이렇게 하면 $z=\eta$를 $z=0$으로 바꿀 수 있다.  또한 선형미분 방정식이 그나마 풀만하기 때문에 선형화 시켜주는 과정이 필요하기도 했다. 또한 일반적으로 파장대비 파고가 매우 작다고 하면, 비선형항을 생략할 수 있다.

$\frac{\partial \varphi }{\partial z}(z=\eta )=\frac{\partial \varphi }{\partial z}+\frac{{\partial }^2\varphi }{\partial z^2}\eta +\dots (z=0)$

$\frac{\partial \eta }{\partial t}-\frac{\partial \varphi }{\partial z}{|}_{z=0}=0$ 로 바꿀 수 있다.

 

 

DBC

자유표면에서의 역학적조건(dynamic free surface boundary condition)은 베르누이 방정식을 이용한 조건이다. 베르누이 방정식은 기본적으로 $\frac{P1}{\rho }+\frac{1}{2}{v}_1^2+g{y}_1=\frac{P2}{\rho }+\frac{1}{2}{v}_2^2+g{y}_2$로 알려져 있다. Unsteady potential flow는 $\frac{\partial \varphi }{\partial t}+\frac{1}{2}|\mathrm{\nabla }\varphi {|}^2+\frac{p_a}{p}+gz=0,z=\eta$로 표현될 수 있다. 여기서 $p_a$는 자유표면에서 대기압이기 때문에 무시할 수 있다. KBC에서와 마찬가지로 비선형항을 무시할 수 있다.

$\frac{\partial \varphi }{\partial t}{|}_{z=0}+g\eta =0$ 

 

CFSBC

합정자유표면조건식("combined kinematic dynamic free surface" or "combined free surface kinematic dynamic")

이는 "KBC"조건과 "DBC"조건을 합친 것이다. DBC를 $t$에 관해 편미분 한 뒤 $\frac{\partial \eta }{\partial t}$를 소거 하면된다.

그 결과 $\frac{{\partial }^2\varphi }{\partial t^2}+g\frac{\partial \varphi }{\partial z}=0$, $z=0$로 표현할 수 있다.

BBC

바닥 경계 조건(bottom boundary condition)도 이용한다. 이는 바닥에서 해파의 수직 방향 속도가 0이라는 조건으로 직관적으로도 납득할만하다. $u_2(x,-h)=\frac{\partial \varphi }{\partial z}{|}_{z=-h}=0$ 이는 평면일 때 가정이고 만약 기울기가 있다면 다른 식으로 해야한다. 여기서는 평면일 때만 하도록 하겠다.

 

LBC(RC, PC)

방사조건(radiation condition)은 해파가 공간적으로나 시간적으로나 반복되는 파동이라는 의미이다.

$\varphi (x,t)=\varphi (x+L,t)=\varphi (x,t+T)$가 되는다는 것이니

$\theta =x-\frac{L}{T}t=x-vt$

 

라플라스 방정식의 해

 

$\varphi (x,z,t)=\varphi (\theta ,z)=Z(z)F(\theta )$ (기존까지의 u는 t가 고정되어 있었다고 생각해야 한다.) 이렇게 바꿀 수 있는 이유는 LBC조건에 의해 파동으로 x와 t의 변수가 필요가 없어지는 것이다. 이제 변수분리법을 이용할 수 있다.

$\frac{{\partial }^2\varphi }{\partial {\theta }^2}+\frac{{\partial }^2\varphi }{\partial z^2}=Z\cdot F^{"}+F\cdot Z^{"}=0$

$\frac{Z^{"}}{Z}=-\frac{F^{"}}{F}=constant=+k^2$

우변을 $+k^2$로 하는 이유는 단순히 이게 결과적으로 더 편하기 때문이다.

$Z=A_1{e}^{kz}+A_2{e}^{-kz}$

$F=B_{1}cosk\theta +B_{2}sink\theta$

각각의 미분 방정식을 풀면 위와 같이 나온다.

 

BBC에 의해 $\frac{\partial \varphi }{\partial z}{|}_{z=-h}=Z^{\prime }(-h)F(\theta )=0$이기 때문에 $Z^{\prime }(0)=0$이다. $\therefore A_1=A_2{e}^{-2k\times (-h)}=A_2{e}^{2kh}$

따라서 $Z=Acoshk(z+h)$로 간단하게 표현가능하다.

$F=Bcos(k\theta +\alpha )$로 바꿀 수 있고 $\alpha$는 $0$으로 설정해도 문제가 생기지 않는다.

$F=Bcos(k(x-ct))=Bcos(kx-wt)$이다.

$\varphi (\theta ,z)=\varphi (x,z,t)=Ccoshk(z+h)\cdot cos(kx-wt)$

 

 

DBC에 의해 $\eta =-\frac{\partial \varphi }{\partial t}{|}_{z=0}\times \frac{1}{g}$임을 알 수 있고, 진폭(a)을 이용하여 C를 구하면 

$\frac{\partial \varphi }{\partial t}{|}_{z=0,max}=Ccoshkhw$, $\therefore C=\frac{ag}{w}\frac{1}{coshkh}$임을 알 수 있다.

따라서 속도포텐셜함수는 $\varphi =\frac{ga}{w}\frac{coshk(z+h)}{coshkh}cos(kx-wt)$로 결정된다.

파형은 $\eta =asin(kx-wt)$이다.

 

일반적인 속도 공식

이렇게 구한 함수를 "CFSBC"에 대입을 해주면 된다.

 

$\frac{{\partial }^2\varphi }{\partial t^2}=\frac{ga}{w}\frac{coshk(z+h)}{coshkh}cos(kx-wt)(-w^2)$

$\frac{\partial \varphi }{\partial z}=\frac{ga}{w}\frac{sinhk(z+h)}{coshkh}(k)cos(kx-wt)$

이를 방정식에 대입하면 $-w^2+gtanh(kh)k=0$이 되고, 

$gktanh(kh)=w^2$가 된다.

 

$w=\frac{2\pi }{T}$ , $k=\frac{2\pi }{L}$이기 때문에 이 또한 대입해주면

$\frac{2\pi g}{L}tanh(\frac{2\pi h}{L})=\frac{4{\pi }^2}{T^2}$

$\frac{gL}{2\pi }tanh(\frac{2\pi h}{L})=\frac{L^2}{T^2}=v^2$

 

 

$\therefore v=\sqrt{\frac{gL}{2\pi }tanh(\frac{2\pi h}{L})}$

이렇게 깊이$h$와 파장$L$을 알고 있으면 해파의 속도를 구할 수 있다.

근사하기

사진2:demos

$tanhx$함수는 사진2처럼 생겼다. 원점에서는 접선의 기울기가 $1$이고, $\pm 1$을 점근선으로 가진다. 

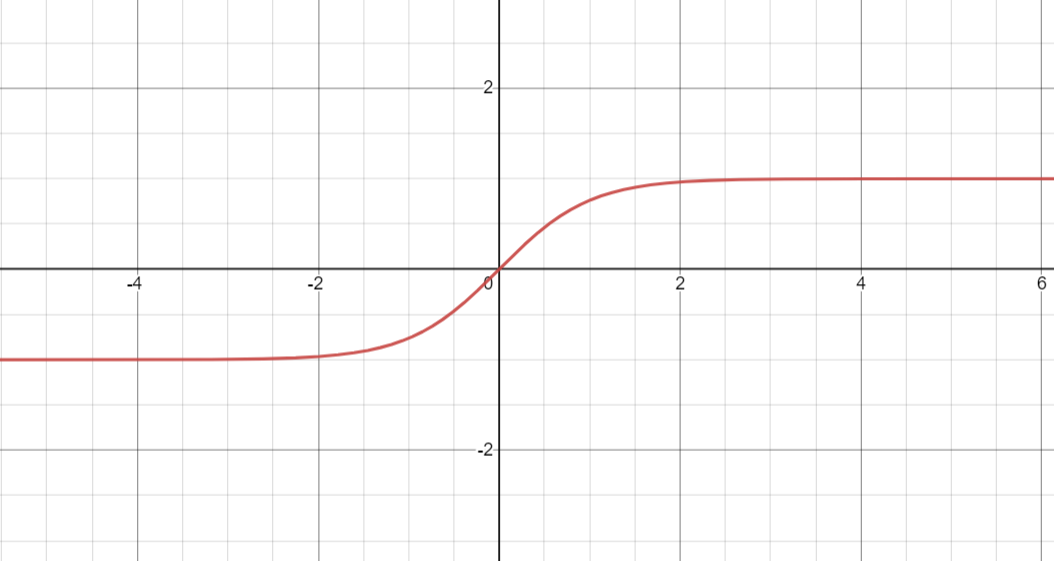
그래서 수심이 굉장히 작거나 커서 $\frac{h}{L}$가 0에 가까우거나 굉장히 클 때, 각각 $tanh(\frac{2\pi h}{L})$이 $\frac{2\pi h}{L},1$로 근사될 수 있으니 각각 해파의 속도는 $\sqrt{gh},\sqrt{\frac{gL}{2\pi }}$로 근사될 수 있다. 이렇게 우리가 배우는 공식을 알 수 있다.

참고

http://contents.kocw.or.kr/KOCW/document/2015/hanyang/choyongsik/04.pdf

http://contents.kocw.or.kr/KOCW/document/2015/hanyang/choyongsik/05.pdf

http://contents.kocw.or.kr/KOCW/document/2015/hanyang/choyongsik/06.pdf

https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=nodong121&logNo=221984241226

https://dms.donga.ac.kr/bbs/civil/324/77206/download.do

https://www.kyungnam.ac.kr/bbs/ship/1017/61412/download.do

https://www.yes24.com/Product/Goods/12185181   

https://en.wikipedia.org/wiki/Bernoulli%27s_principle