(가)에서와 (나)에서 B에 작용하는 힘의 크기는 같고 방향은 반대다. 이때, C의 전하량은 A의 몇 배 인가? 또, A와C 전하의 부호는 같은가? 다른가? (모든 인접한 입자들 사이의 간격은 같다)
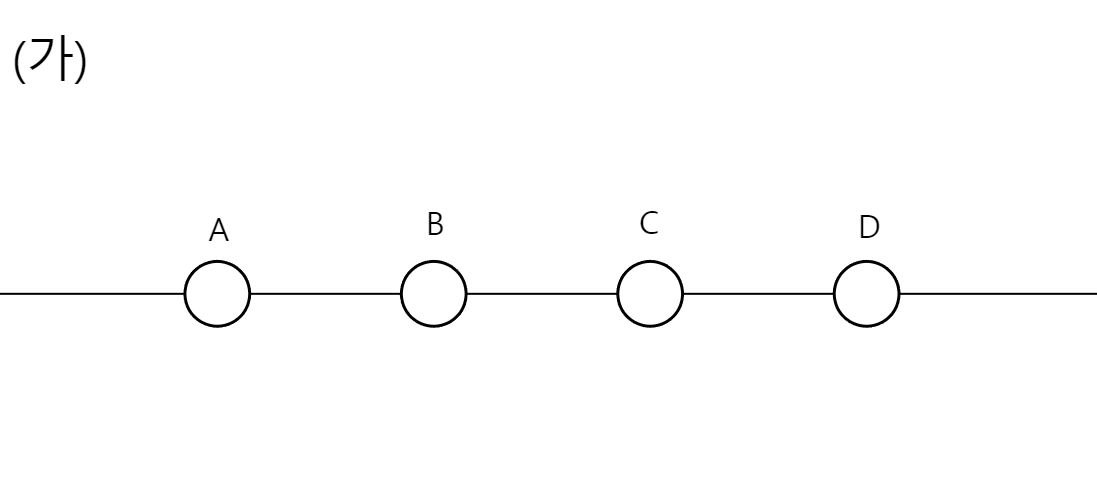
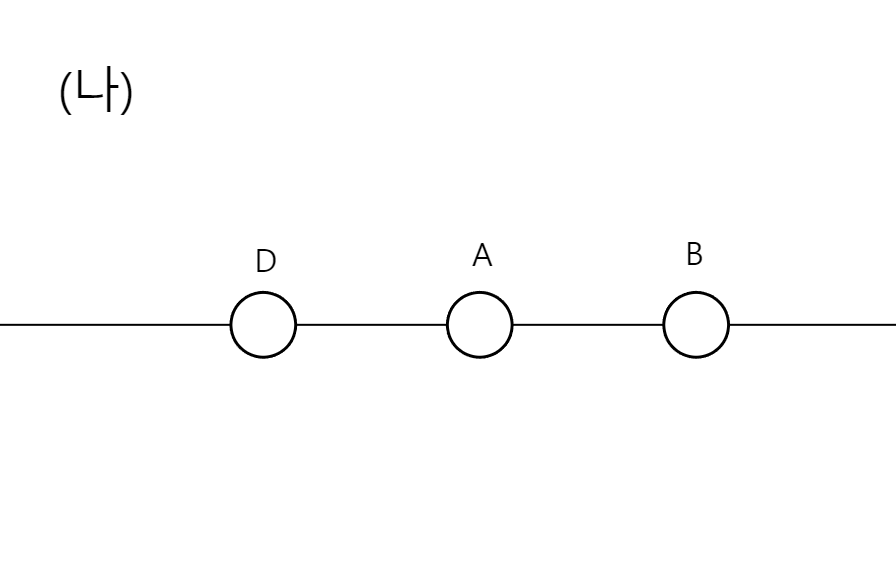
이 문제를 별 생각없이 풀려면 "계산 우당탕"를 해야한다. 그러다 대칭을 이용하여 해결할 수 있다. 이런 비슷한 문제가 엄청 많이 나온다. 그때마다 "두 상황이 딱 대칭적인데, 하나의 상황이 아니라서 대칭은 못쓰겠네"라는 판단을 했었는데, 바로 이 부분을 이용한 것이다.
두 상황을 B를 기준으로 합쳐보는 것이다. 그러면 D는 상쇄가 되고, 왼쪽은 2개의 A가 있고, 오른쪽에는 1개의 C가 있다. 그때 B의 알짜힘은 당연하게 0이 된다. 그럼 C는 A의 2배에 해당하는 전하량을 가지고 있고, 둘은 부호가 같다는 것을 알 수 있다.
이 상황을 다양하게 적용해 볼 수 있다. 0,0인 상황끼리도 합칠 수 있고, -1,2인 상황(전하량을 늘리는 상상이나 전하를 더 추가한다는 상상을 하면 되고, 이때는 그 상황 합섭의 중심이 되는 전하의 전하량을 조심이 조절해야 한다.), 1,1인 상황은 반대로 해서 합성할 수 있다. 이렇게 되면 대칭인 것들이 사라지면서 더 직관적으로 관찰할 수 있게 된다. 이를 수학적으로 보자면 연립 방정식에서 하나의 미지수를 미리 없애는 것과 같은 과정이다.
수험 생활을 하면서 다양한 문제를 봤지만, 해당 조건이 있어도 적용이 잘 안되는 문제도 있고, 다른 풀이가 더 빠를 때도 있었다. 그러나 일부 문제들에서는 우위가 있는 것이 확실하다. Case 분류를 해야하는 상황에서도 안할 수 있었고, 연립방정식을 작성해하는 상황에서도 단순히 하나의 식으로만 해결할 수 있었다. 여기서 전하량을 보정(x=d에서 q와 x=2d에서 4q는 같음)을 이용하면 더 폭 넓게 사용도 가능했다. 그리고 정말 소수의 전류 문제도 이걸로 해결이 가능하긴 하다.(굳이 이렇게 풀 필요는 없긴 하다.) 이 도구를 맹신할 정도는 아니지만, 유용함은 확실하다.
'과학' 카테고리의 다른 글
| [수능 물리학1] 전기 전도도 ,전기 전도율에 대한 오해 (0) | 2024.08.24 |
|---|---|
| 인스타에서 나온 유체 문제 (0) | 2024.06.04 |
| [수능 지구과학2] 해파 속도 (0) | 2023.11.08 |
| [수능 지구과학2] 지각평형의 개념적 해석 (0) | 2023.10.05 |



